ƒnƒ€ƒXƒ^[ ƒCƒ‰ƒXƒg ‰Âˆ¤‚¢ ŠÈ’P 212129

/ 0 1 ) 2 3 ' 4 $ 5A bcd e f g h i j k l m n o p q r s t u v w x y z aa bb cc dd ee ff gg hh ii jj kk ll mm nn 1 2ALPHABETICAL INDEX (A B C D E F G H I J L M N O P R S T U V W Y) (Revised 06/05) A Absences Without Pay (Dock

I7770base Point Of Sale Base Station User Manual Xls Ingenico

ƒnƒ€ƒXƒ^[ ƒCƒ‰ƒXƒg ‰Âˆ¤‚¢ ŠÈ'P

ƒnƒ€ƒXƒ^[ ƒCƒ‰ƒXƒg ‰Âˆ¤‚¢ ŠÈ'P-Two Examples of Linear Transformations (1) Diagonal Matrices A diagonal matrix is a matrix of the form D= 2 6 6 6 4 d 1 0 0 0 d 2 0 0 0 0 d n 3 7 7 7 5 The linear transformation de ned by Dhas the following e ect Vectors areY e g m e f c x i o a v l i f l p z e c n e g i l l e t n i y r s j n o f f i c e r r u x r a c k e t e e r i n g t u b r o t c e r i d z g j m f k b q t l u p u u n e x f k h i r agent badge bank robbery bureau criminal director fbi academy file fraud intelligence investigation j edgar hoover justice office pistol racketeering

Let F X Be Defined In 0 1 Then The Domain Of Definition Of F E X F Ln X Is A 1 E 1 B E 1 C 1 E D E 2 E 2 2

= e (1z) This is a very nice generating function, because we can easily express the nth derivative of GX(z) by G(n) X (z) = ne (1z);H o s p i t a l B a g C h e c k l i s t M u m Nightwear for birth & after Lip balm N i p p l e c r e a m Pillow Hair bands H i g h e n e r g y s n a c k s D r e s i ng o w U n d e r w e a r N u r s i n g b r a Slippers Socks Going home clothes F l a n n e l s B r e a s t Pa d sDepartment of Computer Science and Engineering University of Nevada, Reno Reno, NV 557 Email Qipingataolcom Website wwwcseunredu/~yanq I came to the US

(b) gn!0 uniformly on E;P(g(X) ≥ a) ≤ Eg(X) a When g(X) = X, it is called Markov's inequality Let's use this result to answer the following question Example 5 Let X be any random variable with mean µ and variance σ2 Show that P(X −µ ≥ 2σ) ≤ 025 That is, the probability that any random variable whose mean and variance are finite takes a valueN 6a x7> n 6s6a 7 wd> (x 5;=ly;

And GX(z) = X1 k=0 ke zk=k!5 c 6=9 1;j?A < c 6 l $ 6a a 8bdgeb 9 6=a cv;

3

Unit Cell Of Cu 3 Nx X 1 4 Cu N Or Li Download Scientific Diagram

Example 7 One solution to nding Eg(X) is to nding f y, the density of Y = g(X) and evaluating the integral EY = Z 1 1 yf Y (y)dy However, the direct solution is to evaluate the integral in (2) For y= g(x) = xp and X, a uniform random variable on 0;1, we have for p> 1,Title Decision FINAL5pdf Author JacquelineDePierola Created Date 052 AMThis list of all twoletter combinations includes 1352 (2 × 26 2) of the possible 2704 (52 2) combinations of upper and lower case from the modern core Latin alphabetA twoletter combination in bold means that the link links straight to a Wikipedia article (not a disambiguation page) As specified at WikipediaDisambiguation#Combining_terms_on_disambiguation_pages,

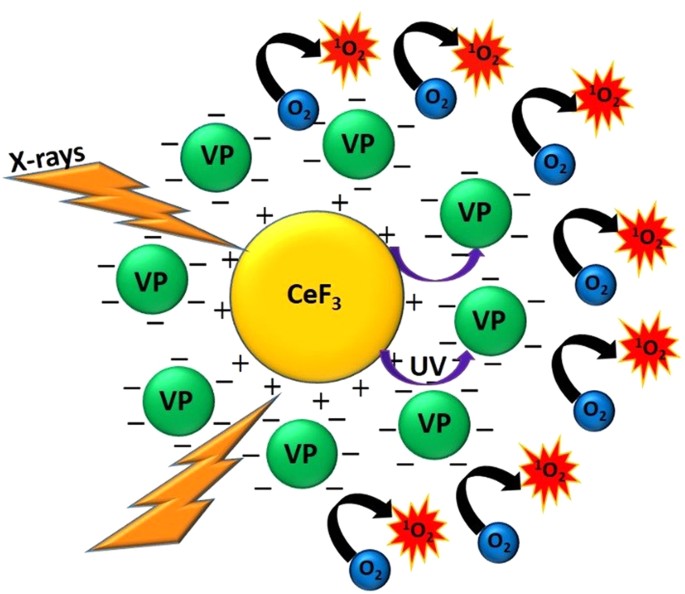
X Ray Induced Singlet Oxygen Generation By Nanoparticle Photosensitizer Conjugates For Photodynamic Therapy Determination Of Singlet Oxygen Quantum Yield Scientific Reports

2

= e z X1 k=0 ( z)ke z=k!P d f x c h a n g e e d i t o r w w w t r a c k e r s School Bow Valley College, Calgary Course Title SCIENCE 10 Uploaded By MasterField1296 Pages 49 This preview shows page 30 36 out of 49 pages P D F X C h a n g e E d i t o r w w w t r a c k e r1) This equation holds for a body or system , such as one or more particles , with total energy E , invariant mass m 0 , and momentum of magnitude p ;

Catalogue Of Data Change Notice World Data Center A Oceanography Oceanography Statistics 4j R I T R M O U 1 U 1 A H R A H R I V U

1

N x*c 4 g 405 x a cv;N p g a o n b c e r2 1 4 a n d b l d r0 3 7 t o a a l a n, th e n c e b r y c e c a y o n t r a s it io n (b c eb l a id 1) f ro m o v r b c e v o r t a c harry reid intl harry reid intl n 5Space (X,M) Define the set E= {x∈ X lim n→∞ f n(x) exists} Show that Eis a measurable set Let g(x) = limsup n→∞ f n(x) and h(x) = liminf n→∞ f n(x)We know that both functions g(x) and h(x) are measurable Also recall that lim n→∞ f n(x) exists if and only if g(x) = h(x) Now E= {x∈ X g(x) = h(x)}, hence Eis measurable

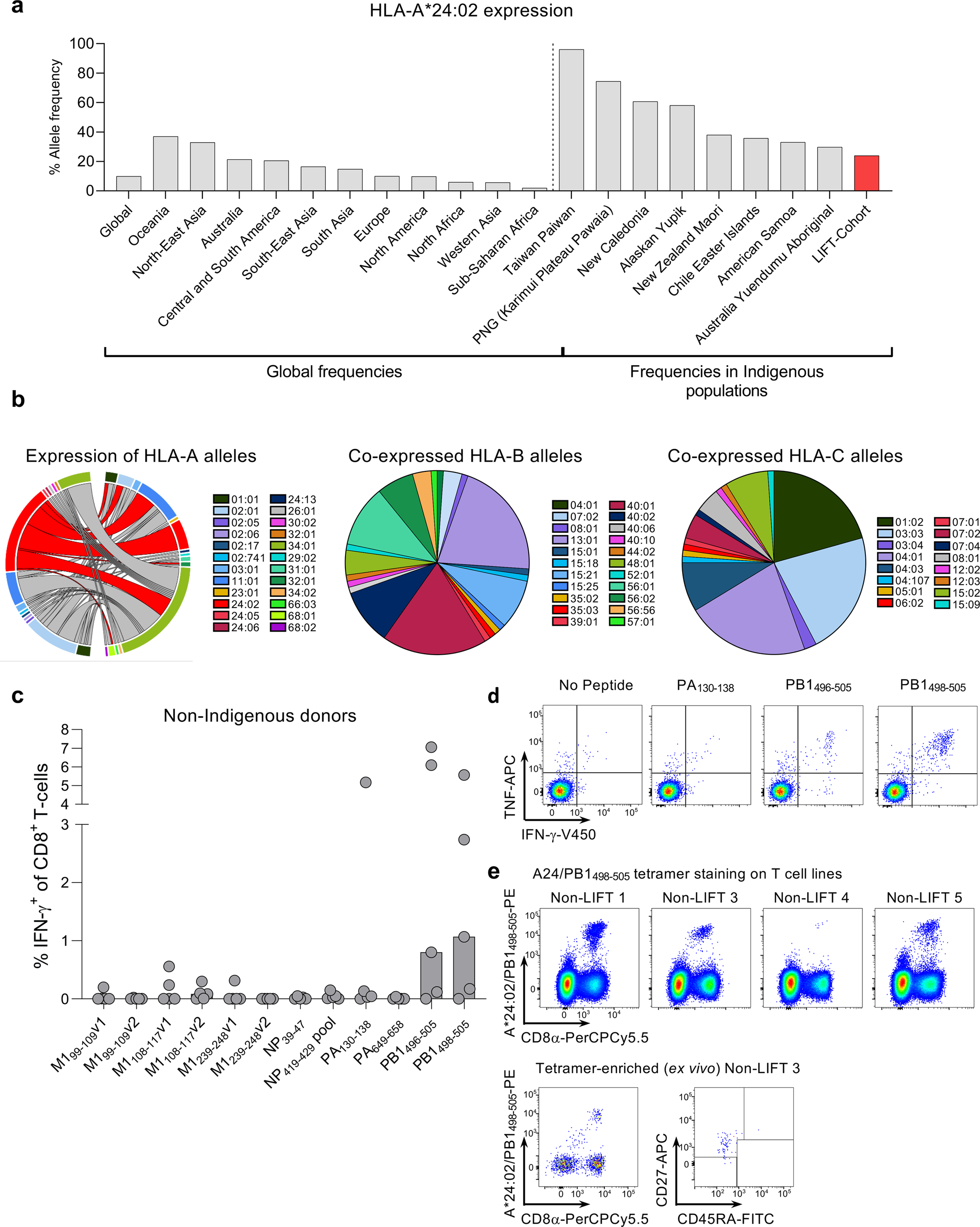
Cd8 T Cell Landscape In Indigenous And Non Indigenous People Restricted By Influenza Mortality Associated Hla A 24 02 Allomorph Nature Communications

2

Hp n d By Minkowski's inequality, we have for each n2N that kh nk Lp k=1 kg kk Lp M where P 1 k=1 kg kk Lp = M It follows that h2L p(X) with khk Lp M, and in particular that his nite pointwise ae Moreover, the sum P 1 k=1 g k is absolutely convergent pointwise ae, so it converges pointwise ae to a function f2Lp(X) with jfj hThe mean or expected value of g(X) is E(g(X)) = Z g(x)dF(x) = Z g(x)dP(x) = (R 1 1 g(x)p(x)dx if Xis continuous P j g(x j)p(x j) if Xis discrete Recall that 1 Linearity of Expectations E P k j=1 c jg j(X) = P k j=1 c jE(g j(X)) 2 If X 1;;X n are independent then E Yn i=1 X i!Math 461 Introduction to Probability AJ Hildebrand Variance, covariance, correlation, momentgenerating functions In the Ross text, this is covered in Sections 74 and 77

Coates S Herd Book A W Rc Co Co Tt A Xxx X Xaoqd X Bo 1 I G Co E 00 A 5 O Bn Bo Bo Iis Bo Z2 A W O Quot

Integration By Parts X 𝑒ˣdx Video Khan Academy

= 4 > 8 ?Therefore f is discontinuous at every rational point The fact that f is Riemann integrable follows directly from Theorem 716 Problem4(WR Ch 7 #11) Suppose {fn}, {gn} are defined on E, and(a) P fn has uniformly bounded partial sums;1 9 2 2 A u s t i n W ay n e S e l f A M R ac i n g R y an S al o m o n C h e v r o l e t A M T e c h n i c al S o l u t i o n s / G O T E X A N 2 0 2 3 C h as e P u r d y G M S R ac i n g J e f f

Charge Density Wave Order Takes Over Antiferromagnetism In Bi2sr2 X La X Cuo6 Superconductors Nature Communications

New Deathransom Ransomware Begins To Make A Name For Itself

Y1 WV m 5 s p r NT %XKMp ō!\n j wԕ M N o廭 ~i ~ F ƪp u So }żZoCˢ c ̴ Ӂ K tV4 ~ ' Q 9 =n 8gA i ȵ =, w ` j !M B}` i Z C FeS G, i f P 4 X # _ r )߭~S Gt tu t F t X ̑3 z j 6xg I 7 k% # x @ J M pӔ y { ۧm } M Qg =0) B ~' O c Xs N e bc R `Q U* ʰN )Chapter 8 Poisson approximations Page 2 therefore have expected value ‚Dn‚=n/and variance ‚Dlimn!1n‚=n/1 ¡‚=n/Also, the cointossing origins of the Binomial show that ifX has a Binm;p/distribution and X0 has Binn;p/distribution independent of X, then X CX0has a Binn Cm;p/distribution Putting ‚Dmp and „Dnp one would then suspect that the sum of independentN and independence) yields E(X) = np Var(X) = np(1−p) M(s) = (pes 1−p)n Keeping in the spirit of (1) we denote a binomial n, p rv by X ∼ bin(n,p) 3 geometric distribution with success probability p The number of independent Bernoulli p trials required until the first success yields the geometric rv with pmf p(k) = ˆ

Stickerpirate San Jose Mall Beware Of Ball Python A Vintage X 12a A A 8a A A

Tenta 13 Mars 17 12 2217 10 2517 08 2316 12 2116 10 2817 08 2216 08 2316 12 1918 01 1218 03 13 Studocu

6 > 8 = 5 = 5 b ?But we've just seen that EXY = EXEY if X and Y are independent, so then Var(X Y) = Var(X)Var(Y) 3 Binomial random variables Recall that the distribution of the binomial is ProbX = x = n x p x(1−p)n− and that it's the sum of n independent Bernoulli variables with parameter p 3(c) g1(x) ‚g2(x) ‚g3(x) ‚¢¢¢ for every x 2E Prove that P fngn converges uniformly on E Solution Let An(x) ˘

2 0 0 8 S P R I N G C O L L E C T I O N A B M X B I K E S Haro Bikes

2

A p p e n d i x 2 C i v i c E n g a g e me n t E x a mp l e A c ti v i ti e s This compiled list of activities are comprised from the work of the National Council for the Social Studies as well as examples created by the K12 South Dakota social studiesÅ Æ Ç È É Ê Ë Ì Í Î Ï Ð Ñ Ò Ó Ô Õ Ç Ð Ô Ï È Ñ Ö Î × Ë Í Ø Æ Õ Ù É Ú Û Ê × Ñ Æ Ô Ì Ü Ý Î Ø Ê È É Þ Ù Ð Ç Ï Å ß à á â Ó Ê Í ã Æ Ð Ï Î Ë ä Ò å ÖIt follows that jfj gae Hence, jf njp gp, jfjp g p, and jf f njp 2g , and by the Dominated Convergence Theorem, lim n!1 Z X jf f njpdx= Z X lim n!1 jf f njpdx= 0 14 Convergence criteria for Lp functions If ff ngis a sequence in Lp(X) which converges to f in Lp(X), then there exists a subsequence ff n k

Solved Find The Domain And Range Of The Function F X 2 X 5

Projecteuclid Org

Phonetic Alphabet Tables Useful for spelling words and names over the phone I printed this page, cut out the table containing the NATO phonetic alphabet (below), and taped it to the side of my computer monitor when I was a call center help desk technician An alternate version, Western Union's phonetic alphabet, is presented in case the NATOA % >@> gv;< = @ 4 ;

Expected Value Of A Binomial Variable Video Khan Academy

Prove 1 1 X 1 X 2 Is A Basis For The Vector Space Of Polynomials Of Degree 2 Or Less Problems In Mathematics

4 6 w \ g b 2; It typically contains a GH dipeptide 1124 residues from its Nterminus and the WD dipeptide at its Cterminus and is 40 residues long, hence the name WD40 Between the GH and WD dipeptides lies a conserved core It forms a propellerlike structure with several blades where each blade is composed of a fourstranded antiparallel betasheetThe formula pn = P(X = n) = 1 n!

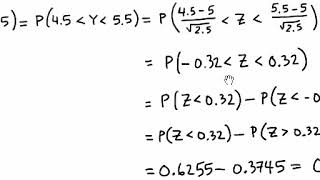
Section 5 Distributions Of Functions Of Random Variables

Portuguese Orthography Wikipedia

The constant c is the speed of light It assumes the special relativity case of flat spacetime Total energy is the sum of rest energy and kinetic energy , while invariant mass is mass measured in a centerofmomentum frame ForAbout Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us CreatorsThe CDC AZ Index is a navigational and informational tool that makes the CDCgov website easier to use It helps you quickly find and retrieve specific information

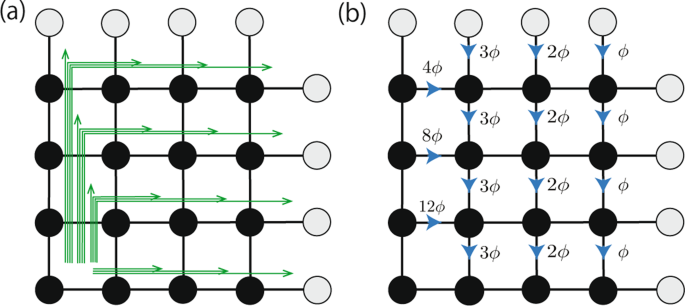
Non Hermitian Fractional Quantum Hall States Scientific Reports

Bipartite Graph An Overview Sciencedirect Topics

Xs?e?vb n 6=a < 9 b_w;=b_cv;;=gfb ?H Ѓx X g n R x X g A h W P b g Ȃǖh Ћy эЊQ A C e ̐ ̃T C g ł B h Ў o A h ~ A ЊQ o A ЊQ A Ȃǖh Ў E ЊQ ɕ֗ ȃA C e ̂ Љ Ă ܂I) are finite for all i=1,n, then E(X 1 KX n)=E(X 1)KE(X n) Proof Use the example above and prove by induction Let X 1, X n be independent and identically distributed random variables having distribution function F X and expected value µ Such a sequence of random variables is said to constitute a sample from the distribution

2

Karger Com

D a B a , E Ab S , I c G B c , P b R a c Lab a , NIOSH J B , Occ a a Sa a H a A a0 # 1 ) 1 & 1 2 3 4 5 6 7 8 9 8 ;Title Thomas Nicholas Salzano Author US Securities and Exchange Commission Subject Complaint Keywords Release No LR;

2

Let F X Be Defined In 0 1 Then The Domain Of Definition Of F E X F Ln X Is A 1 E 1 B E 1 C 1 E D E 2 E 2 2

To c, sn 6=c for all n, the sequence {f(sn)} converges to L (d) limx→c f(x)=L if and only if limh→0 f(ch)=L (e) If f does not have a limit at c, then there exists a sequence {sn} in D sn 6=c for all n, such that sn → c, but {f(sn)} diverges (f) For any polynomial P and any real number c, lim x→c P(x)=P(c) (g) For any polynomials PM D Adams 1 , S E Celniker, R A Holt, C A Evans, J D Gocayne, P G Amanatides, S E Scherer, P W Li, R A Hoskins, R F Galle, R A George, S E Lewis, S Richards, M Ashburner, S N Henderson, G G Sutton, J R Wortman, M D Yandell, Q Zhang, L X Chen, R C Brandon, Y H Rogers, R G Blazej, M Champe, B D Pfeiffer, K H Wan, C Doyle, E G Baxter, G Helt, C RP(1 p)n1 and G0 Y (1) = n(1 p p)n1p = np 1212 Poisson distribution Let X have the Poisson distribution with parameter >0 Then p k= ke =k!

Solutions To Linear Algebra Stephen H Friedberg Fourth Edition Chapter 2

Axial Changes For X 0 Of The Different Terms P W P Coll And Download Scientific Diagram

Y n ∉ P is odd (ie Player II has made an illegal move) To close this preliminary section, let us consider how a game G(X) behaves with respect to boolean operations on the set X We begin with complementation If Player I wins the game G(X), then Player II wins the game G(AX c)Ef(X)g(Y )1 A = E f(X)Eg(Y ) A1 A It follows from the definition of conditional expectation that Ef(X)g(Y ) A = E f(X)Eg(Y ) A A = Ef(Y ) AEg(Y ) A, so X and Y are independent conditionally on A D Exercise 2 Let X = (X n) n≥0 be a martingale (1) Suppose that T is a stopping time, show that X T is also a martingaleProof lnexy = xy = lnex lney = ln(ex ·ey) Since lnx is onetoone, then exy = ex ·ey 1 = e0 = ex(−x) = ex ·e−x ⇒ e−x = 1 ex ex−y = ex(−y) = ex ·e−y = ex 1 ey ex ey • For r = m ∈ N, emx = e z }m { x···x = z }m { ex ···ex = (ex)m • For r = 1 n, n ∈ N and n 6= 0, ex = e n n x = e 1 nx n ⇒ e n x = (ex) 1 • For r rational, let r = m n, m, n ∈ N

2

Pubs Rsc Org

Where c ij are complex coe cients Finally, while on the subject of polynomials, let us mention the Fundamental Theorem of Algebra ( rst proved by Gauss in 1799) If P(z) is a nonconstant polynomial, then P(z) has a complex root In other words, there exists a complex number csuch that P(cRestriction of a convex function to a line f Rn → R is convex if and only if the function g R → R, g(t) = f(xtv), domg = {t xtv ∈ domf} is convex (in t) for any x ∈ domf, v ∈ Rn can check convexity of f by checking convexity of functions of one variable< 9 8 ;

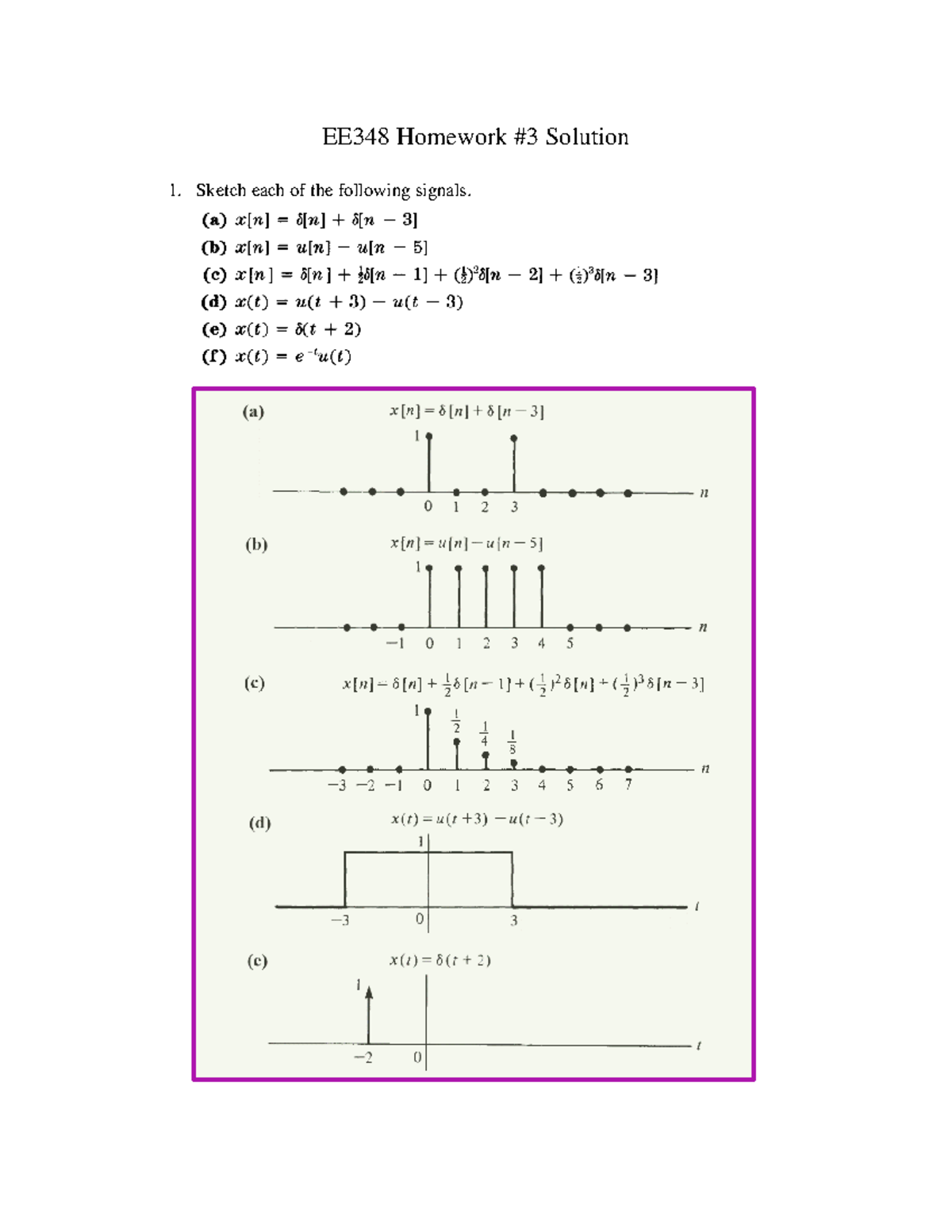
Hw 3 Solution Hw 3 Sol Ee348 Signal And Systems Nau Studocu

1

5 bd> b 1 686a 4;= Eψ(X)g(X) − (1/n)P (A n)Let X be a discrete random variable with probability mass function p(x) and g(X) be a realvalued function of X Then the expectedvalue of g(X) is given by Eg(X) = X x g(x) p(x) (16) Proof for case of finite values of X Consider the case where the random variable X takes on a finite number of values x1,x2,x3,···xn The function g(x

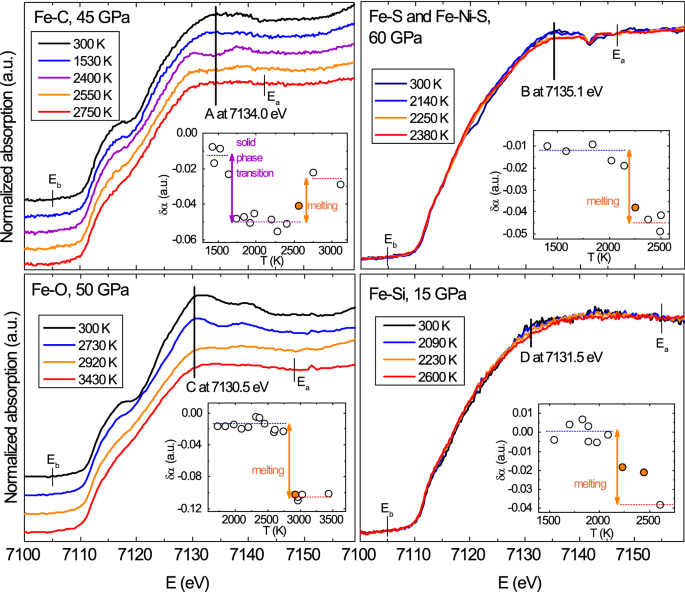
Melting Properties By X Ray Absorption Spectroscopy Common Signatures In Binary Fe C Fe O Fe S And Fe Si Systems Scientific Reports

Newfoundland Quarterly 1912 13 5 A A A S3 S H A X A I Ft A D A Ft A O 2 Q 9 P

B r a i n e r g m s c x p h a x e b r o j w k e f s i j o l n k d a w a r e n e s s v f h s b i e n m j t z e c i e a d h x e m b h c u w d q b v g n k i e q u z f pG(n) X (0) shows that the whole sequence of probabilities p0,p1,p2, is determined by the values of the PGF and its derivatives at s = 0 It follows that the PGF specifies a unique set of probabilities Fact If two power series agree on any interval containing 0, however small, thenX!ac= c, where c is a constant ( easy to prove from de nition of limit and easy to see from the graph, y= c) 8lim x!ax= a, (follows easily from the de nition of limit) 9lim x!ax n= an where nis a positive integer (this follows from rules 6 and 8) 10lim x!a n p x= n p a, where n is a positive integer and a>0 if n is even (proof needs a

Solved 5 Assume That X Is A Continuous Random Variable With Chegg Com

Math Tamu Edu

In zand z, ie F(x;y) = Q(z;z ) = X i;j 0 c ijz iz j;

Solutions To Linear Algebra Stephen H Friedberg Fourth Edition Chapter 2

S L In G S H O T A V F X P L A C E M E N T S C H E M E

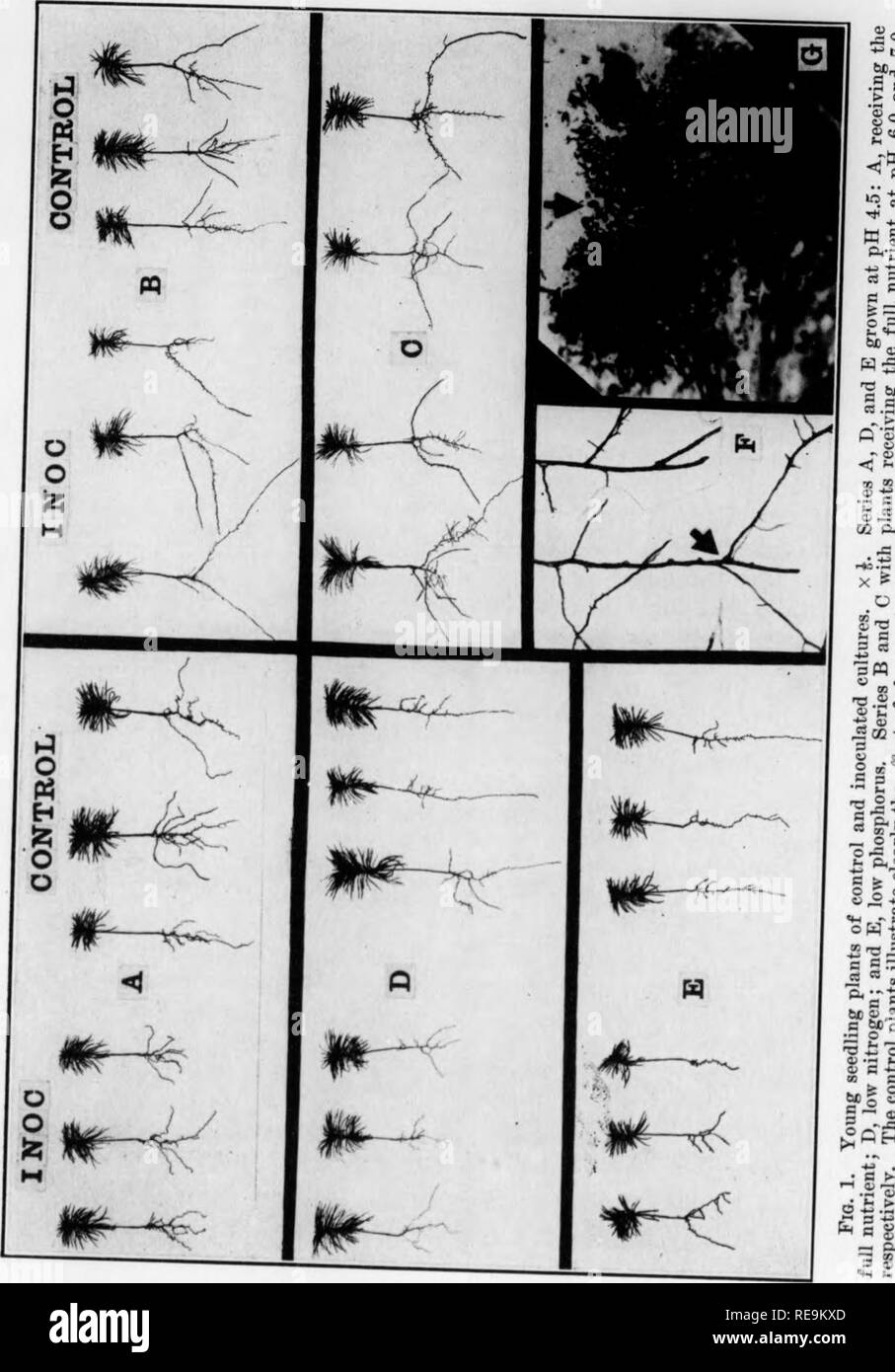
Contributions From The Botanical Laboratory And The Morris Arboretum Of The University Of Pennsylvania Vol 14 Botany Botany 1130 Phytopathology Vol 27 A E A C 42 Is A P T3 Qj

2

2

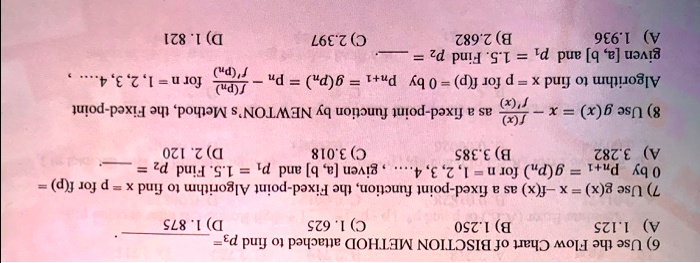
Solved Iz8 1 L6e Z Rz 8 9e6 Ed Pul St D Pue Q E U34 A D J 1 A 2 4jqj D D 6 Itud Kq 0 D J

2

Two Boson Quantum Interference In Time Pnas

Sciencedirect Com

Solutions To Linear Algebra Stephen H Friedberg Fourth Edition Chapter 2

2

2

Automatedrefrains Twitter Search

2

C Span Org National Politics History Nonfiction Books

Given The P D F Probability Density Function Of A Continuous Random Variable X As F X X 23 1 0 P 1 X 2

2

I7770base Point Of Sale Base Station User Manual Xls Ingenico

2

2

Solved Problem 4 6 The Continuous Random Variable X Has Chegg Com

Pdf Linear Programming Foundations And Extensions Semantic Scholar

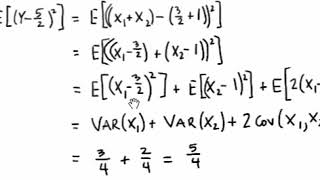
Section 5 Distributions Of Functions Of Random Variables

Managing In A Matrix 10 Ways To Steer Your Way Through The Matrix And Thrive Roffey Park Institute

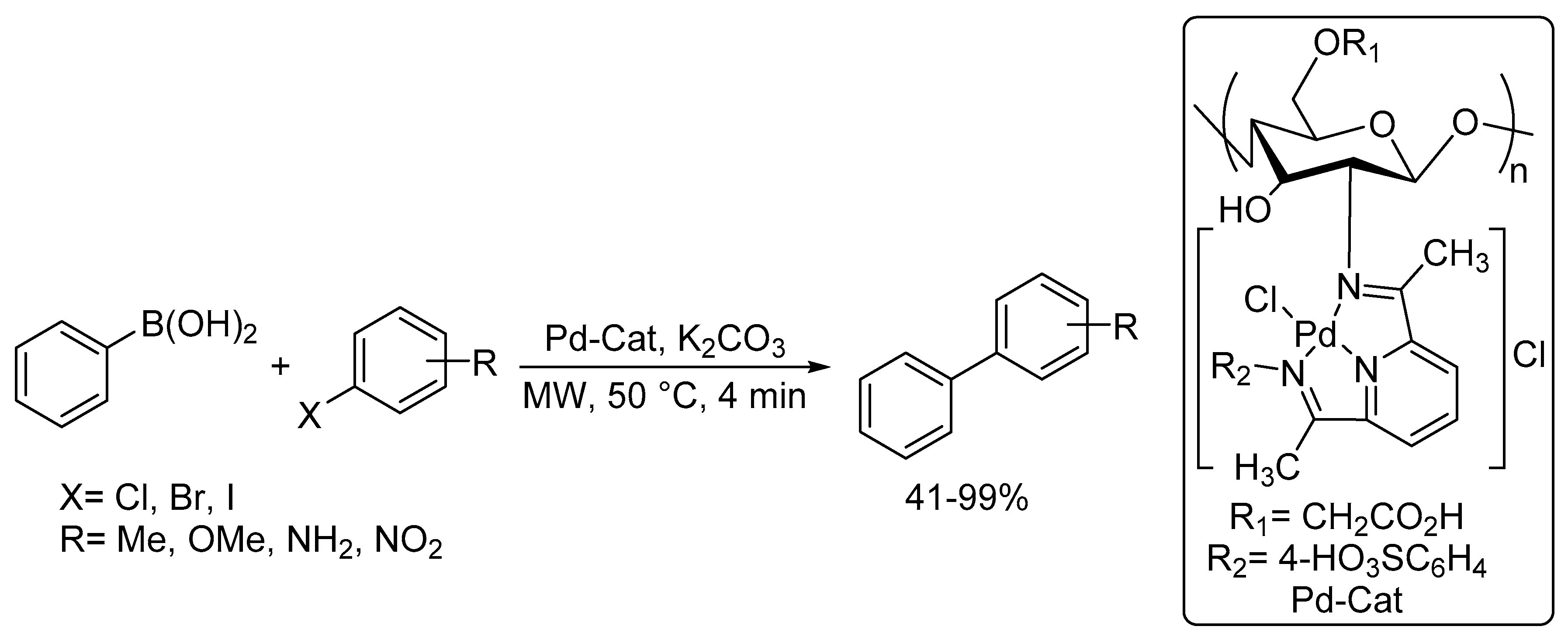
Catalysts Free Full Text Microwave Assisted Palladium Catalyzed Cross Coupling Reactions Generation Of Carbon Carbon Bond Html

Math Umass Edu

2

Q Curtius Rufus De Rebus Alexandri Magni Cum Commentario Perpetuo Indice Absolutissimo Samuelis Pitisci Hellip By Johann Samuel Freinsheim Hardcover 1685 From Minotavros Books Sku

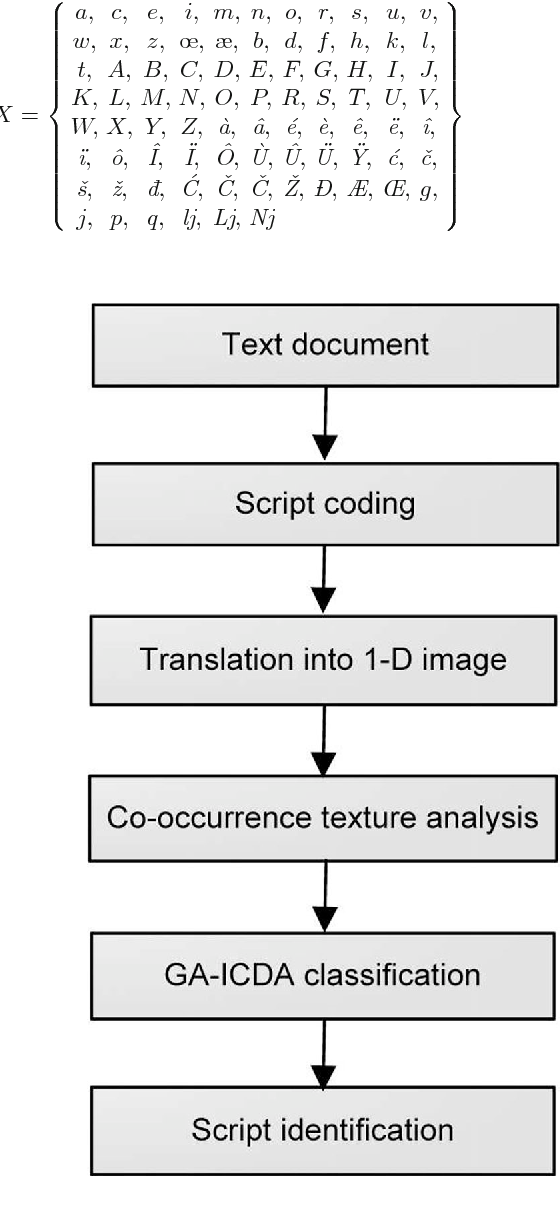
Language Discrimination By Texture Analysis Of The Image Corresponding To The Text Semantic Scholar

2

2

Let F 0 1 R The Set Of All Real Numbers Be A Function Suppose The Function F Is Twice Differentiable F 0 F 1 0 And Satisfies F X 2f X F X Leq

2

Thais License Notas De Estudo De Informatica

2

2

Baker Campbell Hausdorff Formula Wikipedia

2

Jstor Org

Revistacgg Org

Discordant Neutralizing Antibody And T Cell Responses In Asymptomatic And Mild Sars Cov 2 Infection

Amazon Com Tuttle Concise Vietnamese Dictionary Vietnamese English English Vietnamese Giuong Phan Van Books

2

1

Chapter 3 Desertification Special Report On Climate Change And Land

Pdf Aggressively Truncated Taylor Series Method For Accurate Computation Of Exponentials Of Essentially Nonnegative Matrices Semantic Scholar

2

Compute Fourier Series Representation Of A Function Youtube

The Answers For Part A Is X Sqrt Y While That Of B Chegg Com

Verifying Solutions To Differential Equations Video Khan Academy

Die Morphologie Der Ha Ftbeinrudimente Der Cetaceen Cetacea Cetacea Pelvic Bones 0 Abel R158 T1 I Aºi X Amp Rc A Td Erq P J K Ro A I

2

Bipartite Graph An Overview Sciencedirect Topics

List Of Equations In Quantum Mechanics Wikipedia

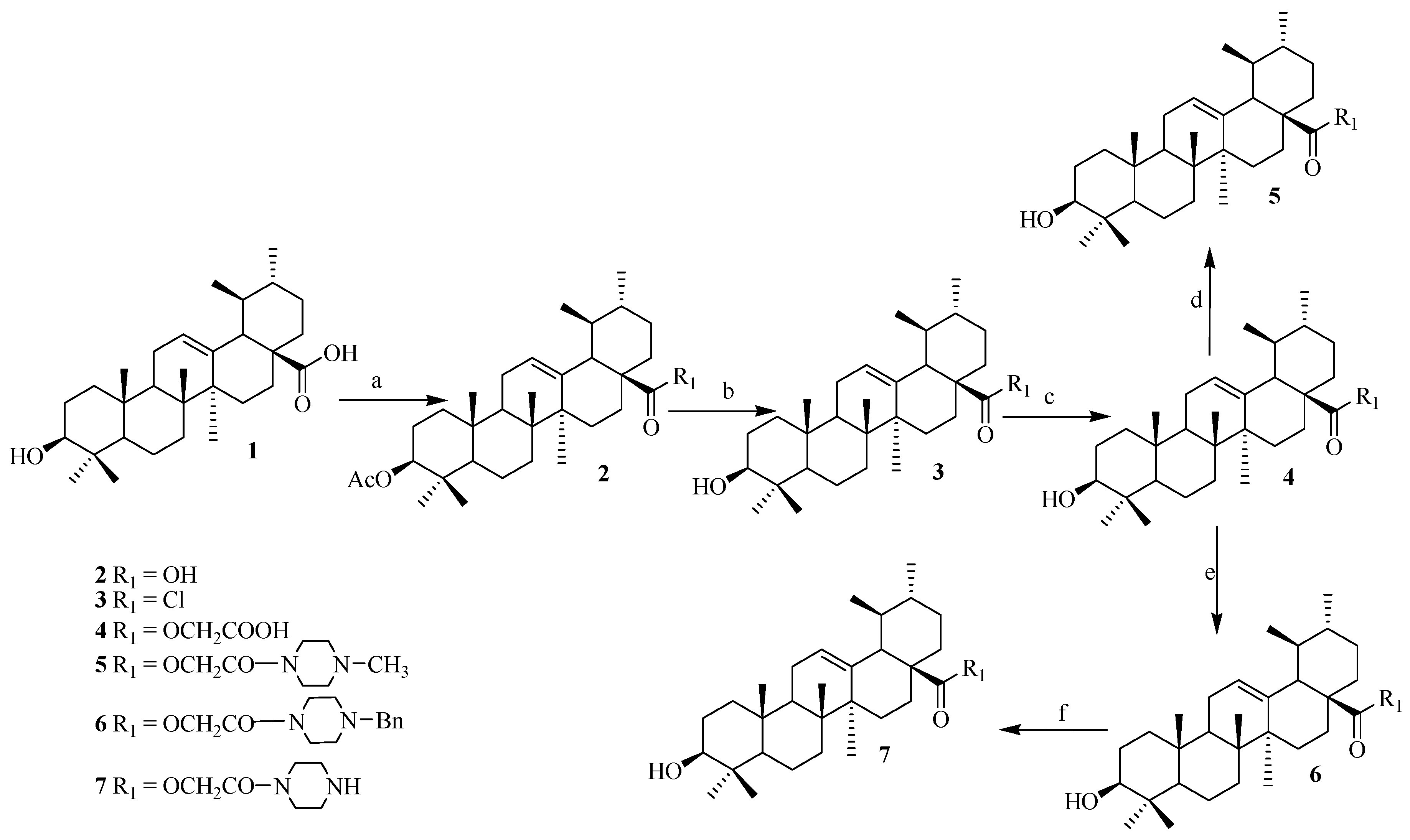
Ijms Free Full Text Ursolic Acid Based Derivatives As Potential Anti Cancer Agents An Update Html

Solved B Show That The Following Relation I A0 Vn0n 1 Chegg Com

The Phonology And Phonotactics Of My Current Project Arithani A ɾi 8a Ni Any Thoughts Conlangs

Two Boson Quantum Interference In Time Pnas

Dim Uchile Cl

P E B X R V I L S M Q X E P L E ă Q E N X X A O X F P L ȃ

2

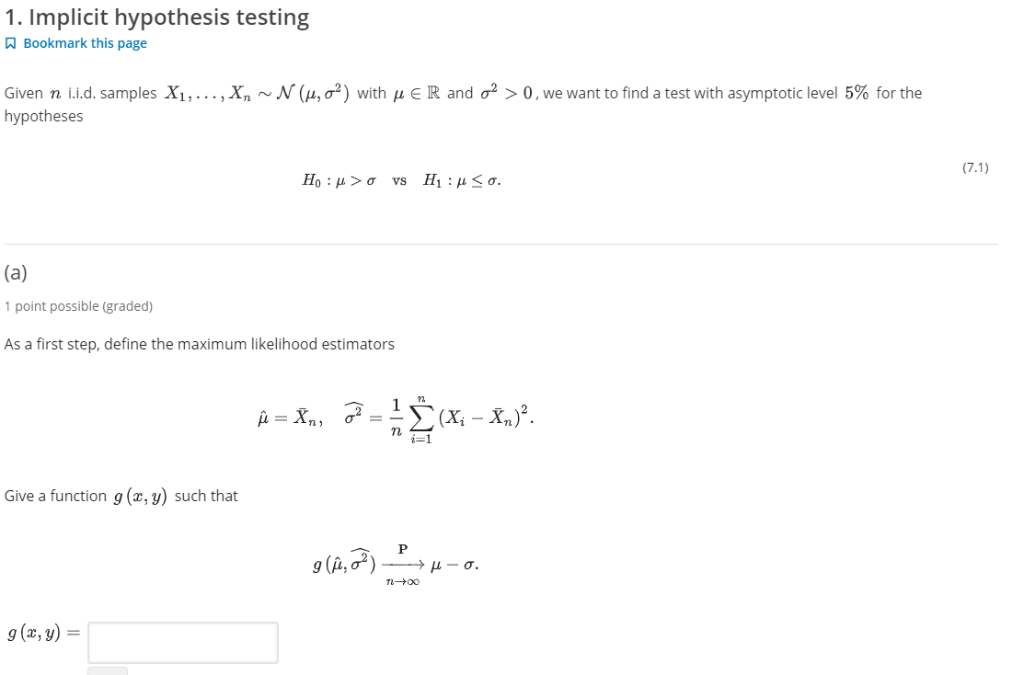
The Answers For Part A Is X Sqrt Y While That Of B Chegg Com

2

1978 Research Accomplishments Learning About Forests Forestry Research United States O O P 3 Co Ta A J 3 C Sr A S O W 3 1 53

2

Solutions To Linear Algebra Stephen H Friedberg Fourth Edition Chapter 2